Here, we discuss the chi-squared contingency table tests of homogeneity and independence in R: interpretations, chi-squared value, expected values, p-values and critical values.

The chi-squared contingency table test in R can be performed with the chisq.test() function from the base "stats" package.

The chi-squared contingency table test of independence can be used to test whether the row variable (with \(r\geq2\) rows) and column variable (with \(c\geq2\) columns) in a contingency table are independent as stated in the null hypothesis.

Also, the chi-squared contingency table test of homogeneity can be used to test whether different populations (with \(r\geq2\) populations) have the same proportions of a categorical variable (with \(c\geq2\) categories) as stated in the null hypothesis.

In the chi-squared contingency table test, the test statistic follows a chi-squared distribution with \((r − 1)(c − 1)\) degrees of freedom when the null hypothesis is true.

Chi-squared Contingency Table Tests & Hypotheses
Question Test of Independence: Are the row and column variables independent? Test of Homogeneity: Are the populations homogeneous?
Null Hypothesis, \(H_0\) The row and column variables are independent, hence, the row (column) cell proportions are equal for all rows (columns). The populations are homogeneous, hence, they have the same proportions for the categories of the categorical variable.
Alternate Hypothesis, \(H_1\) The row and column variables are dependent, hence, at least one row’s (or column’s) cell proportions are different. The populations are not homogeneous, hence, at least one population has different proportions for the categories of the categorical variable.


Sample Steps to Run a Chi-squared Contingency Table Test:

2x2 Two-way Contingency Table
Gender \ Response Yes No Total
Male 45 55 100
Female 60 65 125
Total 105 120 225 
# Create the data for the chi-squared contingency table test
data = rbind(c(45, 55), c(60, 65))

# Run the chi-squared contingency table test with specifications
chisq.test(data, correct = FALSE)

    Pearson's Chi-squared test

data:  data
X-squared = 0.20089, df = 1, p-value = 0.654

Or:

# Create the data for the chi-squared contingency table test
male = c(yes = 45, no = 55)
female = c(yes = 60, no = 65)
rbind(male, female)

# Run the chi-squared contingency table test with specifications
chisq.test(rbind(male, female),
           correct = FALSE)

Or:

# Create the data for the chi-squared contingency table test
x = c(rep("Male", 100), rep("Female", 125))
y = c(rep("Yes", 45), rep("No", 55),
      rep("Yes", 60), rep("No", 65))
table(x, y)
data.frame(x, y)

# Run the chi-squared contingency table test with specifications
chisq.test(x, y,
           correct = FALSE)
Table of Some Chi-squared Contingency Table Tests Arguments in R
Argument Usage
x Matrix of values
y For x as a factor, y will be a factor of the same length
correct Set to FALSE to remove continuity correction (default = TRUE)

Creating a Chi-squared Contingency Table Test Object: 

# Create object
chsq_object = chisq.test(rbind(c(45, 55), c(60, 65)),
                         correct = FALSE)

# Extract a component
chsq_object$statistic
X-squared 
0.2008929
Table of Some Chi-squared Contingency Table Test Object Outputs in R
Test Component Usage
chsq_object$statistic Test-statistic value
chsq_object$p.value P-value
chsq_object$parameter Degrees of freedom
chsq_object$observed Observed counts
chsq_object$expected Expected counts
chsq_object$residuals Residual as (Obs. - Exp.)/sqrt(Exp.)

1 Test Statistic for Chi-squared Contingency Table Test in R

The chi-squared contingency table test has test statistics (correct = FALSE for 2x2 table) that takes the form:

\[\chi^2=\sum_{ij}\frac{(O_{ij}-E_{ij})^2}{E_{ij}}.\]

In cases where Yates’ continuity correction is applied which is the default in R for chisq.test() with 2x2 tables and also only applies to 2x2 tables, it takes the form:

\[\chi^2=\sum_{ij}\frac{(|O_{ij}-E_{ij}|-c)^2}{E_{ij}}.\] With \(r\) rows and \(c\) columns, when the null hypothesis is true, \(\chi^2\) follows a chi-squared distribution (\(\chi^2_{(r-1)(c-1)}\)) with degrees of freedom, \(df = (r-1)(c-1)\),

\(O_{ij}'s\) are the observed values in row \(i\), column \(j\),

\(E_{ij}'s\) are the expected values, \(E_{ij} = \frac{(\text{row $i$ total})(\text{column $j$ total})}{(\text{overall total})}\),

The test is ideal for large samples sizes (for example, each \(E_{ij} > 5\)).

For 2x2 tables, \(c = \min\{0.5, |O_{ij}-E_{ij}|\}\), any cell \(ij\) can be used as \(|O_{ij}-E_{ij}|\) are the same for all cell \(ij\).

See also Fisher’s exact contingency table tests for exact p-values, and chi-squared goodness-of-fit tests.

2 Simple Chi-squared Test of Independence in R

For test of independence between grade and enrollment time among 140 students.

2x2 Two-way Contingency Table
Grade \ Enrollment Early Late Total
Pass 88 32 120
Fail 13 7 20
Total 101 39 140


For the following null hypothesis \(H_0\), and alternative hypothesis \(H_1\), with the level of significance \(\alpha=0.05\), applying continuity correction.

\(H_0:\) the row (grade) and column (enrollment time) variables are independent.

\(H_1:\) the row (grade) and column (enrollment time) variables are dependent.

For 2x2 tables, the chisq.test() function has the default method as continuity corrected, hence, you do not need to specify the "correct" argument in this case.

chisq.test(rbind(c(88, 32), c(13, 7)),
           correct = TRUE)

Or:

chisq.test(rbind(c(88, 32), c(13, 7)))

    Pearson's Chi-squared test with Yates' continuity correction

data:  rbind(c(88, 32), c(13, 7))
X-squared = 0.25028, df = 1, p-value = 0.6169

The test statistic, \(\chi^2_1\), is 0.25028,

the degree of freedom is 1,

the p-value, \(p\), is 0.6169.

Interpretation:

  • P-value: With the p-value (\(p = 0.6169\)) being greater than the level of significance 0.05, we fail to reject the null hypothesis that the row (grade) and column (enrollment time) variables are independent. Hence, enrollment time does not impact grade.

  • \(\chi^2_1\) T-statistic: With test statistics value (\(\chi^2_1 = 0.25028\)) being less than the critical value, \(\chi^2_{1,\alpha}=\text{qchisq(0.95, 1)}=3.8414588\) (or not in the shaded region), we fail to reject the null hypothesis that the row (grade) and column (enrollment time) variables are independent. Hence, enrollment time does not impact grade.

x = seq(0.01, 8, 1/1000); y = dchisq(x, df=1)
plot(x, y, type = "l",
     xlim = c(0, 8), ylim = c(-0.1, min(max(y), 1)),
     main = "Chi-squared Test of Independence
Shaded Region for Simple Test",
     xlab = "x", ylab = "Density",
     lwd = 2, col = "blue")
abline(h=0)
# Add shaded region and legend
point = qchisq(0.95, 1)
polygon(x = c(x[x >= point], 8, point),
        y = c(y[x >= point], 0, 0),
        col = "blue")
legend("topright", c("Area = 0.05"),
       fill = c("blue"), inset = 0.01)
# Add critical value and chi-value
arrows(2.5, 0.4, 0.25028, 0)
text(2.5, 0.45, "chi-squared = 0.25028")
text(3.841459, -0.06, expression(chi[1][','][alpha]^2==3.841459))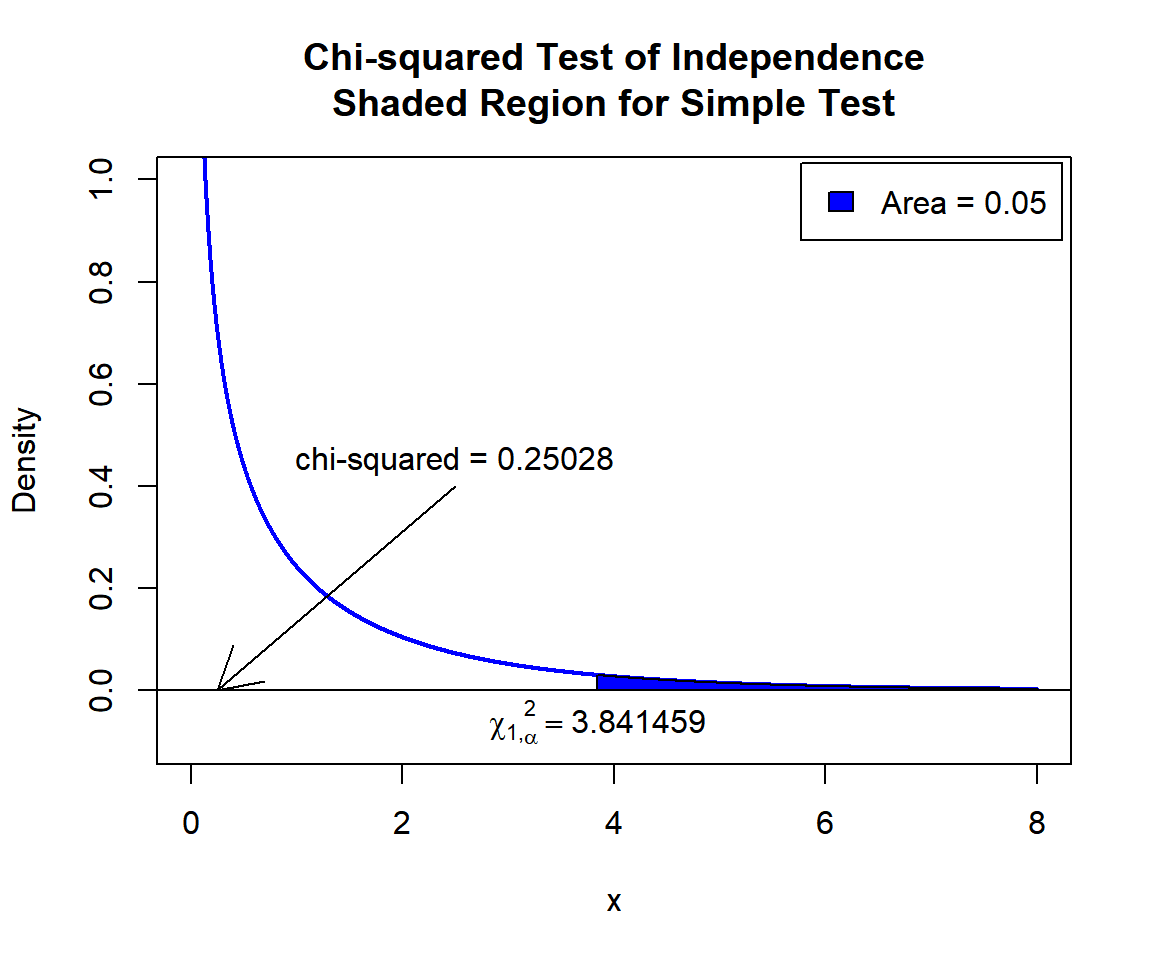
Chi-squared Test of Independence Shaded Region for Simple Test in R

Chi-squared Test of Independence Shaded Region for Simple Test in R

See line charts, shading areas under a curve, lines & arrows on plots, mathematical expressions on plots, and legends on plots for more details on making the plot above.

3 Chi-squared Contingency Table Test Critical Value in R

To get the critical value for a chi-squared test in R, you can use the qchisq() function for chi-squared distribution to derive the quantile associated with the given level of significance value \(\alpha\).

The critical value is qchisq(\(1-\alpha\), df).

Example:

For \(\alpha = 0.1\), and \(\text{df} = 2\).

qchisq(0.9, 2)
[1] 4.60517

4 Chi-squared Test of Homogeneity (3x4 Table) in R

For test whether different age groups are homogeneous with regards to coffee preference.

3x4 Two-way Contingency Table
Age \ Coffee Black Latte Irish Mocha Total
18 to 25 12 44 67 80 203
26 to 45 18 64 97 117 296
Above 45 15 19 27 33 94
Total 45 127 191 230 593


For the following null hypothesis \(H_0\), and alternative hypothesis \(H_1\), with the level of significance \(\alpha=0.1\).

\(H_0:\) the populations (age groups) are homogeneous.

\(H_1:\) the populations (age groups) are not homogeneous.

chisq.test(rbind(c(12, 44, 67, 80),
                 c(18, 64, 97, 117),
                 c(15, 19, 27, 33)))

    Pearson's Chi-squared test

data:  rbind(c(12, 44, 67, 80), c(18, 64, 97, 117), c(15, 19, 27, 33))
X-squared = 11.204, df = 6, p-value = 0.08227

Interpretation:

  • P-value: With the p-value (\(p = 0.08227\)) being less than the level of significance 0.1, we reject the null hypothesis that the populations (age groups) are homogeneous. Hence, there are preferences based on age.

  • \(\chi^2_6\) T-statistic: With test statistics value (\(\chi^2_6 = 11.204\)) being in the critical region (shaded area), that is, \(\chi^2_6 = 11.204\) greater than \(\chi^2_{6, \alpha}=\text{qchisq(0.9, 6)}=10.6446407\), we reject the null hypothesis that the populations (age groups) are homogeneous. Hence, there are preferences based on age.

x = seq(0.01, 25, 1/1000); y = dchisq(x, df=6)
plot(x, y, type = "l",
     xlim = c(0, 25), ylim = c(-0.01, min(max(y), 1)),
     main = "Chi-squared Test of Homogeneity
Shaded Region",
     xlab = "x", ylab = "Density",
     lwd = 2, col = "blue")
abline(h=0)
# Add shaded region and legend
point = qchisq(0.9, 6)
polygon(x = c(x[x >= point], 25, point),
        y = c(y[x >= point], 0, 0),
        col = "blue")
legend("topright", c("Area = 0.1"),
       fill = c("blue"), inset = 0.01)
# Add critical value and chi-value
arrows(15, 0.05, 11.204, 0)
text(15, 0.055, "chi-squared = 11.204")
text(10.64464, -0.006, expression(chi[6][','][alpha]^2==10.64464))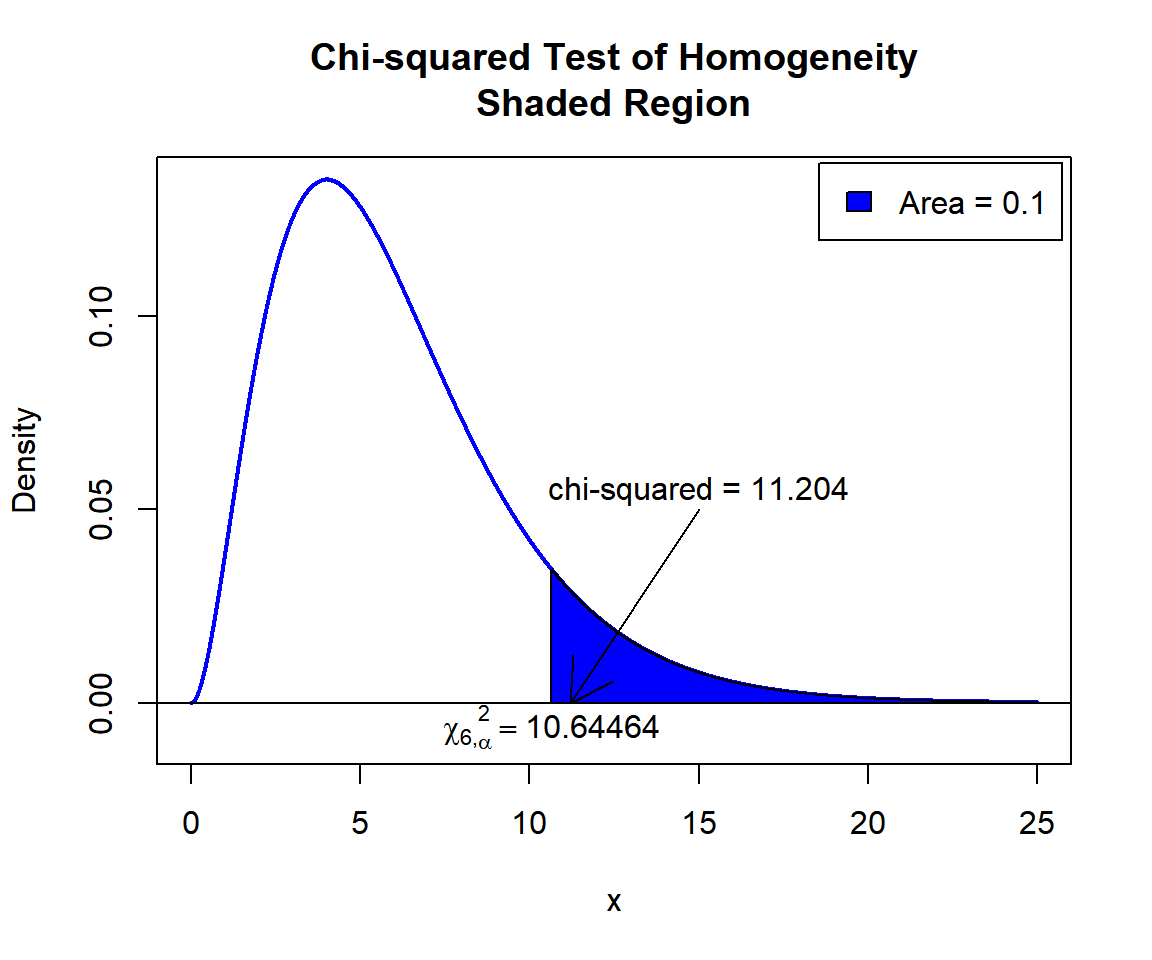
Chi-squared Test of Homogeneity Shaded Region for in R

Chi-squared Test of Homogeneity Shaded Region for in R

5 Chi-squared Test of Independence (3x3 Table) in R

For test whether height and sleep hours are independent among 62 students.

3x3 Two-way Contingency Table
Height \ Hours 9+ 6 to 8 <6 Total
Tall 7 6 8 21
Medium 6 8 7 21
Short 4 10 6 20
Total 17 24 21 62


For the following null hypothesis \(H_0\), and alternative hypothesis \(H_1\), with the level of significance \(\alpha=0.1\).

\(H_0:\) the row (height) and column (sleep hours) variables are independent.

\(H_1:\) the row (height) and column (sleep hours) variables are dependent.

chisq.test(rbind(c(7, 6, 8),
                 c(6, 8, 7),
                 c(4, 10, 6)))

    Pearson's Chi-squared test

data:  rbind(c(7, 6, 8), c(6, 8, 7), c(4, 10, 6))
X-squared = 2.0987, df = 4, p-value = 0.7176

Interpretation:

  • P-value: With the p-value (\(p = 0.7176\)) being greater than the level of significance 0.1, we fail to reject the null hypothesis that the row (height) and column (sleep hours) variables are independent. Hence, height does not impact sleep hours.

  • \(\chi^2_4\) T-statistic: With test statistics value (\(\chi^2_4 = 2.0987\)) being less than the critical value, \(\chi^2_{4,\alpha}=\text{qchisq(0.9, 4)}=7.7794403\) (or not in the shaded region), we fail to reject the null hypothesis that the row (height) and column (sleep hours) variables are independent. Hence, height does not impact sleep hours.

x = seq(0.01, 15, 1/1000); y = dchisq(x, df=4)
plot(x, y, type = "l",
     xlim = c(0, 15), ylim = c(-0.01, min(max(y), 1)),
     main = "Chi-squared Test of Independence
Shaded Region",
     xlab = "x", ylab = "Density",
     lwd = 2, col = "blue")
abline(h=0)
# Add shaded region and legend
point = qchisq(0.9, 4)
polygon(x = c(x[x >= point], 15, point),
        y = c(y[x >= point], 0, 0),
        col = "blue")
legend("topright", c("Area = 0.1"),
       fill = c("blue"), inset = 0.01)
# Add critical value and chi-value
arrows(3.5, 0.05, 2.0987, 0)
text(3.5, 0.055, "chi-squared = 2.0987")
text(7.77944, -0.008, expression(chi[4][','][alpha]^2==7.77944))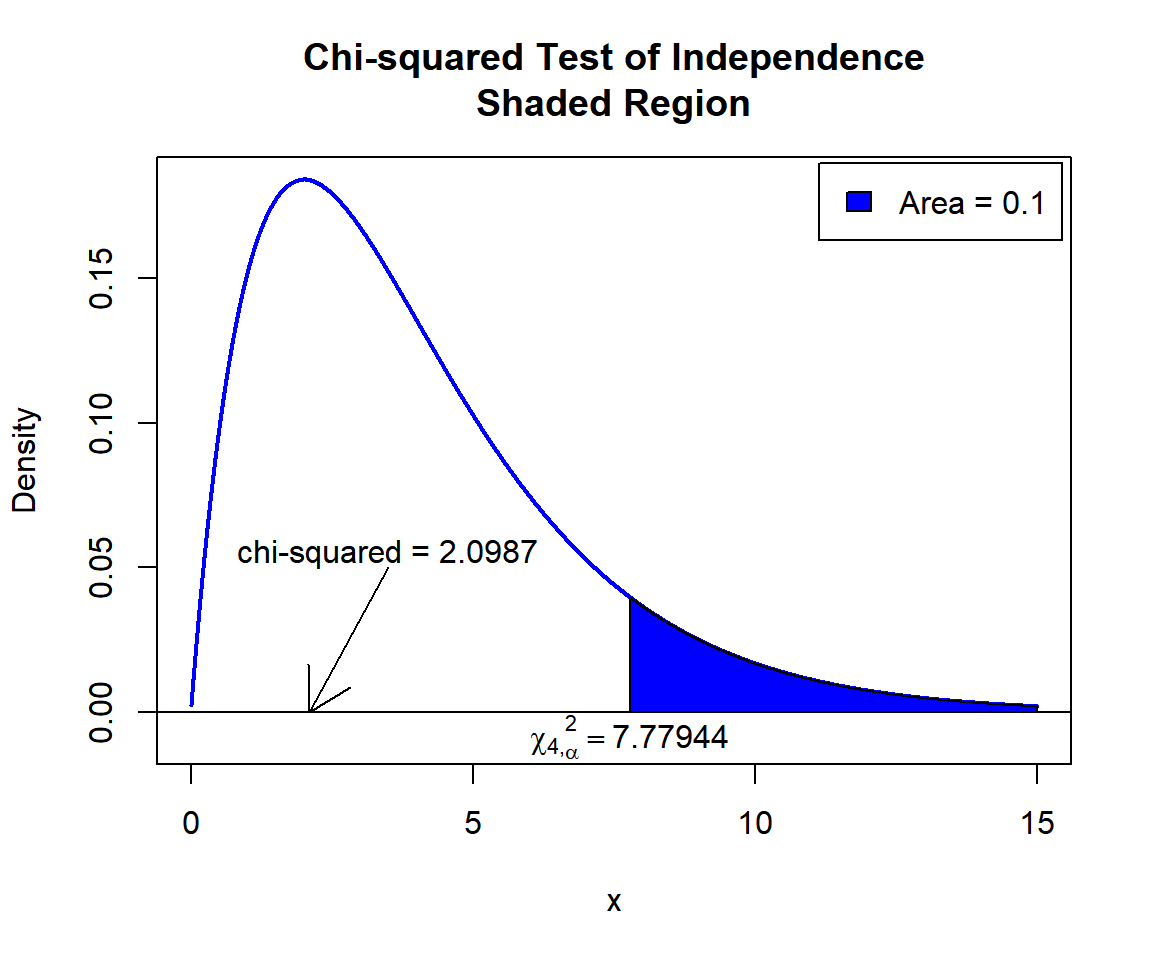
Chi-squared Test of Independence Shaded Region for in R

Chi-squared Test of Independence Shaded Region for in R

6 Chi-squared Contingency Table Test: Test Statistics, P-value & Degree of Freedom in R

Here for a chi-squared contingency table test, we show how to get the test statistics (or chi-squared value), p-values, expected values, and degrees of freedom from the chisq.test() function in R, or by written code.

male = c(yes = 45, no = 55)
female = c(yes = 60, no = 65)
chsq_object = chisq.test(rbind(male, female),
                         correct = TRUE)
chsq_object

    Pearson's Chi-squared test with Yates' continuity correction

data:  rbind(male, female)
X-squared = 0.098437, df = 1, p-value = 0.7537

To get the test statistic or chi-squared value; observed and expected values:

\[\chi^2=\sum_{ij}\frac{(O_{ij}-E_{ij})^2}{E_{ij}},\]

Applicable to 2x2 tables only, for Yates’ continuity correction:

\[\chi^2=\sum_{ij}\frac{(|O_{ij}-E_{ij}|-c)^2}{E_{ij}}.\]

\(c = \min\{0.5, |O_{ij}-E_{ij}|\}\). \(|O_{ij}-E_{ij}|\) is equal for all \(ij\).

chsq_object$statistic
X-squared 
0.0984375 
# to remove name X-squared
unname(chsq_object$statistic)
[1] 0.0984375
chsq_object$observed
       yes no
male    45 55
female  60 65
chsq_object$expected
            yes       no
male   46.66667 53.33333
female 58.33333 66.66667

Same as (with continuity correction):

male = c(yes = 45, no = 55)
female = c(yes = 60, no = 65)
obs = rbind(male, female)
n = sum(obs)
rsum = rowSums(obs)
csum = colSums(obs)
exp = outer(rsum, csum, "*")/n
c = min(0.5, abs(obs-exp))
chi = sum(((abs(obs-exp)-c)^2)/exp)
chi
[1] 0.0984375
obs
       yes no
male    45 55
female  60 65
exp
            yes       no
male   46.66667 53.33333
female 58.33333 66.66667

Without continuity correction:

male = c(yes = 45, no = 55)
female = c(yes = 60, no = 65)
obs = rbind(male, female)
n = sum(obs)
rsum = rowSums(obs)
csum = colSums(obs)
exp = outer(rsum, csum, "*")/n
chi = sum(((obs-exp)^2)/exp)
chi
obs
exp

To get the p-value:

The p-value is, \(P \left(\chi^2_{df}> \text{observed} \right)\)

chsq_object$p.value
[1] 0.7537128

Same as:

Note that the p-value depends on the \(\text{test statistics}\) (\(\chi^2_1 = 0.0984375\)), \(\text{degrees of freedom}\) (1). We also use the distribution function pchisq() for the chi-squared distribution in R.

1-pchisq(0.0984375, 1)
[1] 0.7537128

To get the degrees of freedom:

The degree of freedom is \((r-1)(c-1)\).

chsq_object$parameter
df 
 1 
# to remove name df
unname(chsq_object$parameter)
[1] 1

Same as:

r = nrow(obs)
c = ncol(obs)
(r-1)*(c-1)
[1] 1

Copyright © 2020 - 2024. All Rights Reserved by Stats Codes