Here, we discuss logistic regression in R with interpretations, including coefficients, probability of success, odds ratio, AIC and p-values.

Logistic regression is of the binomial family generalized linear model. Hence, in R, the logistic regression can be performed with the glm() function from the "stats" package in base version of R, specifying the binomial() family and the logit link.

Logistic regression can be used to study the relationship, if they exist, between a Bernoulli or binomial distributed dependent variable \((y)\), and a set of independent variables \((x_1, x_2, \ldots, x_m)\).

The logistic regression is based on the theoretical assumption that:

\[y\sim Bernoulli(p),\]

and \(y\) is connected to \((x_1, x_2, \ldots, x_m)\) through \(p\) with the logit link function:

\[ \log \left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_m x_m + \varepsilon,\]

where \(\varepsilon\) represents the error terms. The logistic regression model then estimates the true coefficients, \(\beta_1, \beta_2, \ldots, \beta_m\), as \(\widehat \beta_1, \widehat \beta_2, \ldots, \widehat \beta_m\), and the true intercept, \(\beta_0\), as \(\widehat \beta_0\).
Then for any \(x_1, x_2, \ldots, x_m\) values, these are used to predict or estimate the true \(p\), as \(\widehat p\), with the equation below:

\[\widehat p = \frac{\exp\left( \widehat \beta_0 + \widehat \beta_1 x_1 + \widehat \beta_2 x_2 + \cdots + \widehat \beta_m x_m \right)}{1 + \exp\left( \widehat \beta_0 + \widehat \beta_1 x_1 + \widehat \beta_2 x_2 + \cdots + \widehat \beta_m x_m \right)}.\]

See also linear regression and multiple regression.

Sample Steps to Run a Logistic Regression Model: 

# Create the data samples for the logistic regression model
# Values are paired based on matching position in each sample

y = c(1, 0, 1, 1, 0, 0,
      0, 1, 1, 0, 1, 0)
x1 = c(5.05, 4.75, 5.03, 5.82, 6.03, 3.59,
       5.55, 4.62, 5.61, 2.85, 7.56, 4.96)
x2 = c(2.79, 3.27, 2.11, 3.03, 3.43, 2.67,
       3.92, 2.53, 3.58, 2.73, 1.22, 3.31)
lgr_data = data.frame(y, x1, x2)
lgr_data

# Run the logistic regression model

model = glm(y ~ x1 + x2, family = binomial())
summary(model)

# Or

model = glm(y ~ x1 + x2, family = binomial(link = "logit"),
            data = lgr_data)
summary(model)
   y   x1   x2
1  1 5.05 2.79
2  0 4.75 3.27
3  1 5.03 2.11
4  1 5.82 3.03
5  0 6.03 3.43
6  0 3.59 2.67
7  0 5.55 3.92
8  1 4.62 2.53
9  1 5.61 3.58
10 0 2.85 2.73
11 1 7.56 1.22
12 0 4.96 3.31

Call:
glm(formula = y ~ x1 + x2, family = binomial())

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)    3.138      8.104   0.387   0.6986  
x1             2.978      1.750   1.702   0.0888 .
x2            -5.907      3.414  -1.730   0.0836 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 16.6355  on 11  degrees of freedom
Residual deviance:  7.1821  on  9  degrees of freedom
AIC: 13.182

Number of Fisher Scoring iterations: 7
Table of Some Logistic Regression Model Arguments in R
Argument Usage
y ~ x1 + x2 +…+ xm y is the dependent sample, and x1, x2, …, xm are the independent samples
y ~ ., data y is the dependent sample, and "." means all other variables are in the model
family = binomial() Sets to binomial family, the link can be set in (), default is "logit"
link Set to binomial(link = "logit"), but not required, default is "logit"
data The dataframe object that contains the dependent and independent variables
weights For binomial variable, with the proportion of success as the dependent variable:
vector of the number of cases for each proportion of success

Creating Logistic Regression Summary Object and Model Object: 

# Create data
x1 = rnorm(1000, 3, 1)
x2 = rnorm(1000, 2.5, 0.7)
xb = 1.5 + 2*x1 - 3*x2
p = exp(xb)/(1+exp(xb))
y = rbinom(1000, 1, p)

# Create logistic regression model summary and model objects
lgr_summary = summary(glm(y ~ x1 + x2,  family = binomial()))
lgr_model = glm(y ~ x1 + x2, family = binomial())
# Extract a component from logistic regression summary object
lgr_summary$coefficients; lgr_summary$coefficients[, 1]
             Estimate Std. Error    z value     Pr(>|z|)
(Intercept)  1.843634  0.4382976   4.206352 2.595263e-05
x1           1.944994  0.1412202  13.772777 3.716496e-43
x2          -3.007622  0.2104453 -14.291707 2.464921e-46
(Intercept)          x1          x2 
   1.843634    1.944994   -3.007622 
# Extract a component from logistic regression model object
lgr_model$coefficients
(Intercept)          x1          x2 
   1.843634    1.944994   -3.007622

There are more examples in the table below.

Table of Some Logistic Regression Summary and Model Object Outputs in R
GLM Component Usage
lgr_model$coefficients The estimated intercept and beta values
lgr_model$fitted.values The predicted probability values
lgr_model$linear.predictors The predicted linear model values
lgr_model$residuals The linear model residuals
lgr_model$aic The Akaike’s An Information Criterion value
lgr_model$null.deviance The null model’s deviance
lgr_model$deviance The model’s deviance
lgr_model$df.residual The model’s residual degrees of freedom
lgr_model$df.null The null model’s residual degrees of freedom
lgr_model$model The model dataframe
lgr_summary$coefficients The estimated intercept and beta values:
their standard error, z-value and p-value
lgr_summary$aic The Akaike’s An Information Criterion value
lgr_summary$null.deviance The null model’s deviance
lgr_summary$deviance The model’s deviance
lgr_summary$df.residual The model’s residual degrees of freedom
lgr_summary$df.null The null model’s residual degrees of freedom

1 Logistic Regression with Single Variable in R

Using the "mtcars" data from the "datasets" package with 10 sample rows below:

mtcars
                    mpg cyl  disp  hp drat    wt  qsec vs am gear carb
Mazda RX4          21.0   6 160.0 110 3.90 2.620 16.46  0  1    4    4
Datsun 710         22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
Valiant            18.1   6 225.0 105 2.76 3.460 20.22  1  0    3    1
Cadillac Fleetwood 10.4   8 472.0 205 2.93 5.250 17.98  0  0    3    4
Chrysler Imperial  14.7   8 440.0 230 3.23 5.345 17.42  0  0    3    4
Camaro Z28         13.3   8 350.0 245 3.73 3.840 15.41  0  0    3    4
Fiat X1-9          27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
Porsche 914-2      26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2
Maserati Bora      15.0   8 301.0 335 3.54 3.570 14.60  0  1    5    8
Volvo 142E         21.4   4 121.0 109 4.11 2.780 18.60  1  1    4    2

NOTE: The dependent variable is "vs", which is engine type: 0 = V-shaped, and 1 = straight. The independent variable is "qsec", the time to reach a quarter mile.

1.1 Check for Relationship

Use a box plot to visually check for a relationship.

qsec = mtcars$qsec
vs = mtcars$vs
boxplot(qsec ~ vs,
     main = "Box Plot for Logistic Regression in R")
Box Plot for Logistic Regression in R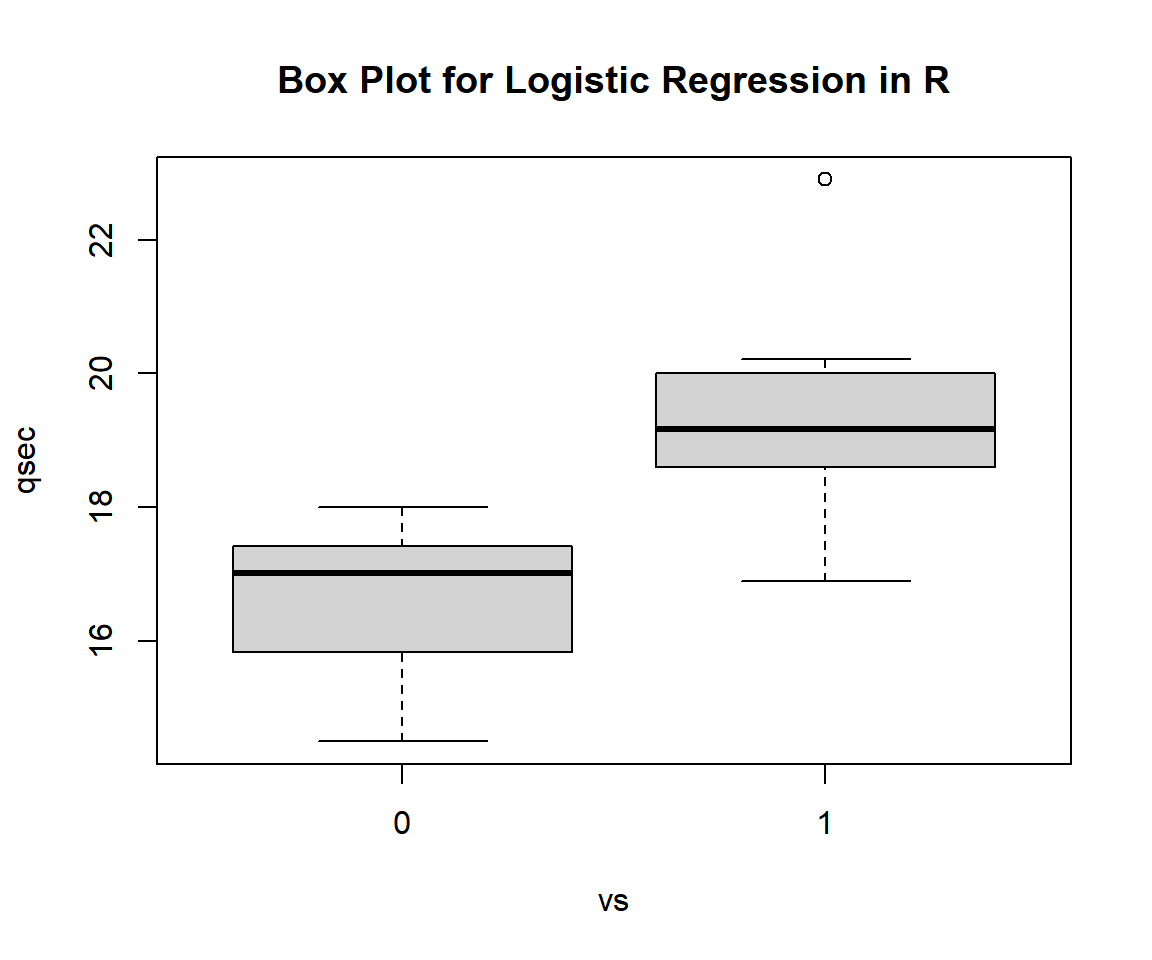

Box Plot for Logistic Regression in R

The appearance of the boxplot suggests a strong relationship between "vs" and "qsec". The box for "1" or "straight" shaped engine appears significantly higher.

1.2 Run the Logistic Regression

Run the single variable logistic regression model using the glm() function and family = binomial(), and print the results using the summary() function.

vs = mtcars$vs
qsec = mtcars$qsec
model = glm(vs ~ qsec, family = binomial())
summary(model)

Or:

model = glm(vs ~ qsec, family = binomial(),
            data = mtcars)
summary(model)

Call:
glm(formula = vs ~ qsec, family = binomial(), data = mtcars)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)   
(Intercept)  -56.361     21.455  -2.627  0.00862 **
qsec           3.123      1.192   2.619  0.00881 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 43.860  on 31  degrees of freedom
Residual deviance: 14.076  on 30  degrees of freedom
AIC: 18.076

Number of Fisher Scoring iterations: 7

1.3 Interpretation of the Results

  • Coefficients:
    • The estimated intercept (\(\widehat \beta_0\)) is \(\text{summary(model)\$coefficients[1, 1]}\) \(= -56.36123\).
    • The estimated coefficient for \(x\) (\(\widehat \beta_1\)) is \(\text{summary(model)\$coefficients[2, 1]}\) \(= 3.1229\).
  • P-values:
    For level of significance, \(\alpha = 0.05\).
    • The p-value for the independent variable, \(x\) ("qsec"), is \(\text{summary(model)\$coefficients[2, 4]}\) \(= 0.0088134\). Since the p-value is less than \(0.05\), we say that the independent variable is a statistically significant predictor of the dependent variable \(y\) ("vs").
      If the p-value were higher than the chosen level of significance, we would have concluded otherwise.
  • AIC:
    The AIC value is \(\text{summary(model)\$aic}\) \(= 18.076\).
    When comparing the model to other models for predicting "vs" based on the same data, the model with a lower AIC is better.

1.4 Odds and Odds Ratio

With \(p_{vs} = \text{Probability(vs = 1)}\).

\(\log \left(\frac{\widehat p_{vs}}{1- \widehat p_{vs}} \right)\) \(= \widehat \beta_0 + \widehat \beta_1 \times qsec\) \(= -56.36123 + 3.1229 \times qsec.\)

Odds:

Hence, the odds, \(\frac{\widehat p_{vs}}{1 - \widehat p_{vs}}\), is \(\exp \left( -56.36123 + 3.1229 \times qsec \right).\)

Therefore, for 1 unit increase in \(x\) ("qsec"), the odds is multiplied by (or increases by a factor of) \(\exp (3.1229)\) = \(22.712\).

Odds Ratio:

For two different values of "qsecs", \(x_1\) and \(x_2\), the odds ratio, \(\left(\frac{\widehat p_{vs\_x2}}{1 - \widehat p_{vs\_x2}}\right)/\left(\frac{\widehat p_{vs\_x1}}{1 - \widehat p_{vs\_x1}}\right)\), is \(\exp (3.1229 \times x_2) / \exp (3.1229 \times x_1).\)

1.5 Prediction and Estimation

With \(p_{vs} = \text{Probability(vs = 1)}\).

\(\widehat p_{vs}\) \(= \frac{\exp (-56.36123 \; + \; 3.1229 \times qsec)}{1 + \exp (-56.36123 \; + \; 3.1229 \times qsec)}\).

For example, for \(x = 18\) (qsec = 18), \(\widehat p_{vs}\) \(= \frac{\exp (-56.36123 \; + \; 3.1229 \times 18)}{1 \; + \; \exp (-56.36123 \; + \; 3.122896 \times 18)}\) \(= \frac{\exp (-0.149)}{1 \; + \; \exp (-0.149)}\) \(= 0.463\).

With \(\widehat p_{vs} = 0.463\), which is less than \(0.5\), we should predict \(vs = 0\), that is, engine is V-shaped.

2 Logistic Regression with Categorical Independent Variable in R

Using the same "mtcars" data from the "datasets" package above.

mtcars

NOTE: The dependent variable is "am", which is transmission type: 0 = automatic, and 1 = manual. The categorical independent variable is "cyl", which is number of cylinders category: 4, 6, or 8.

am = mtcars$am
cyl = mtcars$cyl
am_data = data.frame(am, cyl)
table(am_data)
   cyl
am   4  6  8
  0  3  4 12
  1  8  3  2

The table of "am" versus "cyl" shows that the higher the "cyl", the more likely it is that "am = 0", and the lower the "cyl", the more likely it is that "am = 1".

Run the Logistic Regression

Run the categorical independent variable logistic regression model using the glm() function and family = binomial(), and print the results using the summary() function.

Setting "cyl" as a factor helps treat it as a categorical variable instead of a numeric variable.

am = mtcars$am
cyl = factor(mtcars$cyl)
model = glm(am ~ cyl, family = binomial())
summary(model)

Or:

model = glm(am ~ factor(cyl), family = binomial(),
            data = mtcars)
summary(model)

Call:
glm(formula = am ~ factor(cyl), family = binomial(), data = mtcars)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)   
(Intercept)    0.9808     0.6770   1.449   0.1474   
factor(cyl)6  -1.2685     1.0206  -1.243   0.2139   
factor(cyl)8  -2.7726     1.0206  -2.717   0.0066 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 43.230  on 31  degrees of freedom
Residual deviance: 33.935  on 29  degrees of freedom
AIC: 39.935

Number of Fisher Scoring iterations: 4

Interpretation of the Results

  • Coefficients:
    • The estimated coefficient for "4 cylinders" is the intercept, \(\text{summary(model)\$coefficients[1, 1]}\) \(= 0.98083\).
    • The estimated effect of "6 cylinders" versus "4 cylinders" is \(\text{summary(model)\$coefficients[2, 1]}\) \(= -1.26851\).
    • The estimated effect of "8 cylinders" versus "4 cylinders" is \(\text{summary(model)\$coefficients[3, 1]}\) \(= -2.77259\).
  • P-values:
    For level of significance, \(\alpha = 0.05\).
    • The p-value for the intercept ("4 cylinders"), is \(\text{summary(model)\$coefficients[1, 4]}\) \(= 0.1474\). Since the p-value is greater than \(0.05\), we say that the log(odds of automatic transmission = "1") with "4 cylinders" is NOT statistically different from 0, or the probability of success (automatic transmission = "1") with "4 cylinders" is NOT statistically different from 0.5 (50-50 guess).
    • The p-value for "6 cylinders" effect is \(\text{summary(model)\$coefficients[2, 4]}\) \(= 0.21391\). Since the p-value is greater than \(0.05\), we say that the log(odds of automatic transmission = "1") for "6 cylinders" is NOT statistically significantly different from that of "4 cylinders", or the probability of success (automatic transmission = "1") with "6 cylinders" is NOT statistically different from that of "4 cylinders".
    • The p-value for "8 cylinders" effect is \(\text{summary(model)\$coefficients[3, 4]}\) \(= 0.0066\). Since the p-value is less than \(0.05\), we say that the log(odds of automatic transmission = "1") for "8 cylinders" is statistically significantly different from that of "4 cylinders", or the probability of success (automatic transmission = "1") with "8 cylinders" is statistically different from that of "4 cylinders".
  • AIC:
    The AIC value is \(\text{summary(model)\$aic}\) \(= 39.935\).
    When comparing the model to other models for predicting "am" based on the same data, the model with a lower AIC is better.

Odds and Odds Ratio

With \(p_{am} = \text{Probability(am = 1)}\).

\(\log \left(\frac{\widehat p_{am}}{1- \widehat p_{am}} \right)\) \(= \widehat \beta_{intercept} + \widehat \beta_{category}.\)

Hence, the odds, \(\frac{\widehat p_{am}}{1 - \widehat p_{am}}\), are:

  • "4 cylinders": \(\frac{\widehat p_{am}}{1 - \widehat p_{am}}\) \(= \exp \left( 0.98083 \right)\) \(= 2.667.\)

  • "6 cylinders": \(\frac{\widehat p_{am}}{1 - \widehat p_{am}}\) \(= \exp \left( 0.98083 + (-1.26851) \right)\) \(=\exp \left( -0.2877 \right)\) \(= 0.75.\)

  • "8 cylinders": \(\frac{\widehat p_{am}}{1 - \widehat p_{am}}\) \(= \exp \left( 0.98083 + (-2.77259) \right)\) \(=\exp \left( -1.7918 \right)\) \(= 0.167.\)

Also, the odds ratio, \(\left(\frac{\widehat p_{am\_*cyl}}{1 - \widehat p_{am\_*cyl}}\right)/\left(\frac{\widehat p_{am\_4cyl}}{1 - \widehat p_{am\_4cyl}}\right)\), are:

  • "6 cylinders" versus "4 cylinders": \(\left(\frac{\widehat p_{am\_6cyl}}{1 - \widehat p_{am\_6cyl}}\right)/\left(\frac{\widehat p_{am\_4cyl}}{1 - \widehat p_{am\_4cyl}}\right)\) \(= \exp \left(-1.26851\right)\) \(= 0.281.\)

  • "8 cylinders" versus "4 cylinders": \(\left(\frac{\widehat p_{am\_8cyl}}{1 - \widehat p_{am\_8cyl}}\right)/\left(\frac{\widehat p_{am\_4cyl}}{1 - \widehat p_{am\_4cyl}}\right)\) \(= \exp \left(-2.77259\right)\) \(= 0.063.\)

Prediction and Estimation

With \(p_{am} = \text{Probability(am = 1)}\).

  • "4 cylinders": \(\widehat p_{am}\) \(= \frac{\exp \left( 0.9808 \right)}{1 \; + \; \exp \left( 0.9808 \right)}\) \(= 0.727.\)

  • "6 cylinders": \(\widehat p_{am}\) \(=\frac{\exp \left( -0.2877 \right)}{1 \; + \; \exp \left( -0.2877 \right)}\) \(= 0.429.\)

  • "8 cylinders": \(\widehat p_{am}\) \(=\frac{\exp \left( -1.7918 \right)}{1 \; + \; \exp \left( -1.7918 \right)}\) \(= 0.143.\)

Hence, we predict \(am = 1\) (automatic transmission = "1") for "4 cylinders" since \(0.727\) is greater than \(0.5\).

Also, we predict \(am = 0\) (automatic transmission = "0") for "6 cylinders" and "8 cylinders" since \(0.429\) and \(0.143\) are less than \(0.5\).

3 Logistic Regression with Numeric & Categorical Independent Variables in R

Using the same "mtcars" data from the "datasets" package above.

mtcars

NOTE: The dependent variable is "vs", which is engine type: 0 = V-shaped, and 1 = straight. The independent variables are "wt", weight in 1000lbs, and "am", which is transmission type: 0 = automatic, and 1 = manual.

Run the Logistic Regression

Run the logistic regression model with numeric and categorical independent variables using the glm() function and family = binomial(), and print the results using the summary() function.

Setting "am" as a factor helps treat it as a categorical variable instead of a numeric variable.

vs = mtcars$vs
wt = mtcars$wt
am = factor(mtcars$am)
model = glm(vs ~ wt + am, family = binomial())
summary(model)

Or:

model = glm(vs ~ wt + factor(am), family = binomial(),
            data = mtcars)
summary(model)

Call:
glm(formula = vs ~ wt + factor(am), family = binomial(), data = mtcars)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)   
(Intercept)   21.751      8.433   2.579  0.00991 **
wt            -6.330      2.425  -2.611  0.00904 **
factor(am)1   -6.133      2.700  -2.272  0.02312 * 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 43.860  on 31  degrees of freedom
Residual deviance: 21.532  on 29  degrees of freedom
AIC: 27.532

Number of Fisher Scoring iterations: 7

Interpretation of the Results

  • Coefficients:
    • The estimated coefficient for "(am)0 - automatic" is the intercept, \(\text{summary(model)\$coefficients[1, 1]}\) \(= 21.75053\).
    • The estimated coefficient for "wt" is \(\text{summary(model)\$coefficients[2, 1]}\) \(= -6.32969\).
    • The estimated effect of "(am)1 - manual" versus "(am)0 - automatic" is \(\text{summary(model)\$coefficients[3, 1]}\) \(= -6.13349\).
  • P-values:
    For level of significance, \(\alpha = 0.05\).
    • The p-value for the intercept ("(am)0 - automatic"), is \(\text{summary(model)\$coefficients[1, 4]}\) \(= 0.00991\). Since the p-value is less than \(0.05\), we say that the log(odds of V-shaped engine = "1") with "(am)0 - automatic" and "wt = 0" is statistically different from 0, or the probability of success (V-shaped engine = "1") with "(am)0 - automatic" and "wt = 0" is statistically different from 0.5 (50-50 guess).
    • The p-value for "wt" is \(\text{summary(model)\$coefficients[2, 4]}\) \(= 0.00904\). Since the p-value is less than \(0.05\), we say that "wt" is a statistically significant predictor of the log(odds of V-shaped engine = "1") or probability of success (V-shape = "1”).
    • The p-value for "(am)1 - manual" effect is \(\text{summary(model)\$coefficients[3, 4]}\) \(= 0.02312\). Since the p-value is less than \(0.05\), we say that, for any given "wt" value, the log(odds of V-shaped engine = "1") for "(am)1 - manual" is statistically significantly different from that of "(am)0 - automatic". Also, for any given "wt" value, the probability of success (V-shaped engine = "1") with "(am)1 - manual" is statistically different from that of "(am)0 - automatic".
  • AIC:
    The AIC value is \(\text{summary(model)\$aic}\) \(= 27.532\).
    When comparing the model to other models for predicting "vs" based on the same data, the model with a lower AIC is better.

Odds

With \(p_{vs} = \text{Probability(vs = 1)}\).

\(\log \left(\frac{\widehat p_{vs}}{1- \widehat p_{vs}} \right)\) \(= \widehat \beta_{intercept} +\beta_{category} + \widehat \beta_{weight} \times weight.\)

Hence, the odds, \(\frac{\widehat p_{vs}}{1 - \widehat p_{vs}}\), are:

  • For "(am)0 - automatic": \(\frac{\widehat p_{vs}}{1 - \widehat p_{vs}}\) \(= \exp \left( 21.75053 + (-6.32969) \times weight \right).\)

  • For "(am)1 - manual": \(\frac{\widehat p_{vs}}{1 - \widehat p_{vs}}\) \(= \exp \left( 21.75053 + (-6.13349) + (-6.32969) \times weight \right).\)

Hence, for 3000lbs of weight (wt = 3), the odds, \(\frac{\widehat p_{vs}}{1 - \widehat p_{vs}}\), are:

  • For "(am)0 - automatic": \(\frac{\widehat p_{vs}}{1 - \widehat p_{vs}}\) \(= \exp \left( 21.7505 + (-6.32969) \times 3 \right)\) \(=\exp \left( 2.76144 \right)\) \(= 15.823.\)

  • For "(am)1 - manual": \(\frac{\widehat p_{vs}}{1 - \widehat p_{vs}}\) \(= \exp \left( 21.75053 + (-6.13349) + (-6.32969) \times 3 \right)\) \(=\exp \left( -3.372 \right)\) \(= 0.034.\)

Prediction and Estimation

Similarly, for 3000lbs of weight (wt = 3), \(p_{vs} = \text{Probability(vs = 1)}\) are:

  • For "(am)0 - automatic": \(\widehat p_{vs}\) \(= \frac{\exp \left(2.76144 \right)}{1 \; + \; \exp \left(2.76144 \right)}\) \(= 0.941.\)

  • For "(am)1 - manual": \(\widehat p_{vs}\) \(= \frac{\exp \left(-3.372 \right)}{1 \; + \; \exp \left(-3.372 \right)}\) \(= 0.0332.\)

Hence, we predict \(vs = 1\) (V-shaped = "1") for "(am)0 - automatic" since \(0.941\) is greater than \(0.5\).

Also, we predict \(vs = 0\) (V-shaped = "0") for "(am)1 - manual" since \(0.0332\) is less than \(0.5\).

4 Logistic Regression with Multiple Independent Variables in R

Using the same "mtcars" data from the "datasets" package above.

mtcars

NOTE: The dependent variable is "am", which is transmission type: 0 = automatic, and 1 = manual. The independent variables are "disp" (displacement (cu.in.)), and "hp" (horsepower).

Run the Logistic Regression

Run the logistic regression model with multiple independent variables using the glm() function and family = binomial(), and print the results using the summary() function.

am = mtcars$am
disp = mtcars$disp
hp = mtcars$hp
model = glm(am ~ disp + hp, family = binomial())
summary(model)

Or:

model = glm(am ~ disp + hp, family = binomial(),
            data = mtcars)
summary(model)

Call:
glm(formula = am ~ disp + hp, family = binomial(), data = mtcars)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  1.40342    1.36757   1.026   0.3048  
disp        -0.09518    0.04800  -1.983   0.0474 *
hp           0.12170    0.06777   1.796   0.0725 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 43.230  on 31  degrees of freedom
Residual deviance: 16.713  on 29  degrees of freedom
AIC: 22.713

Number of Fisher Scoring iterations: 8
b0 = summary(model)$coefficients[1,1]
b1 = summary(model)$coefficients[2,1]
b2 = summary(model)$coefficients[3,1]

am = mtcars$am; disp = mtcars$disp; hp = mtcars$hp
plot(disp, hp, col = (am + 2),
     main = "Plot of Actuals versus Decision Boundary")
segments(x0 = (-b0/b1 - (b2*min(hp))/b1), y0 = min(hp), 
         x1 = (-b0/b1 - (b2*max(hp))/b1), y1 = max(hp),
         col = "blue")
legend("topleft",
       c("0", "1"),
       fill = c("red", "green"))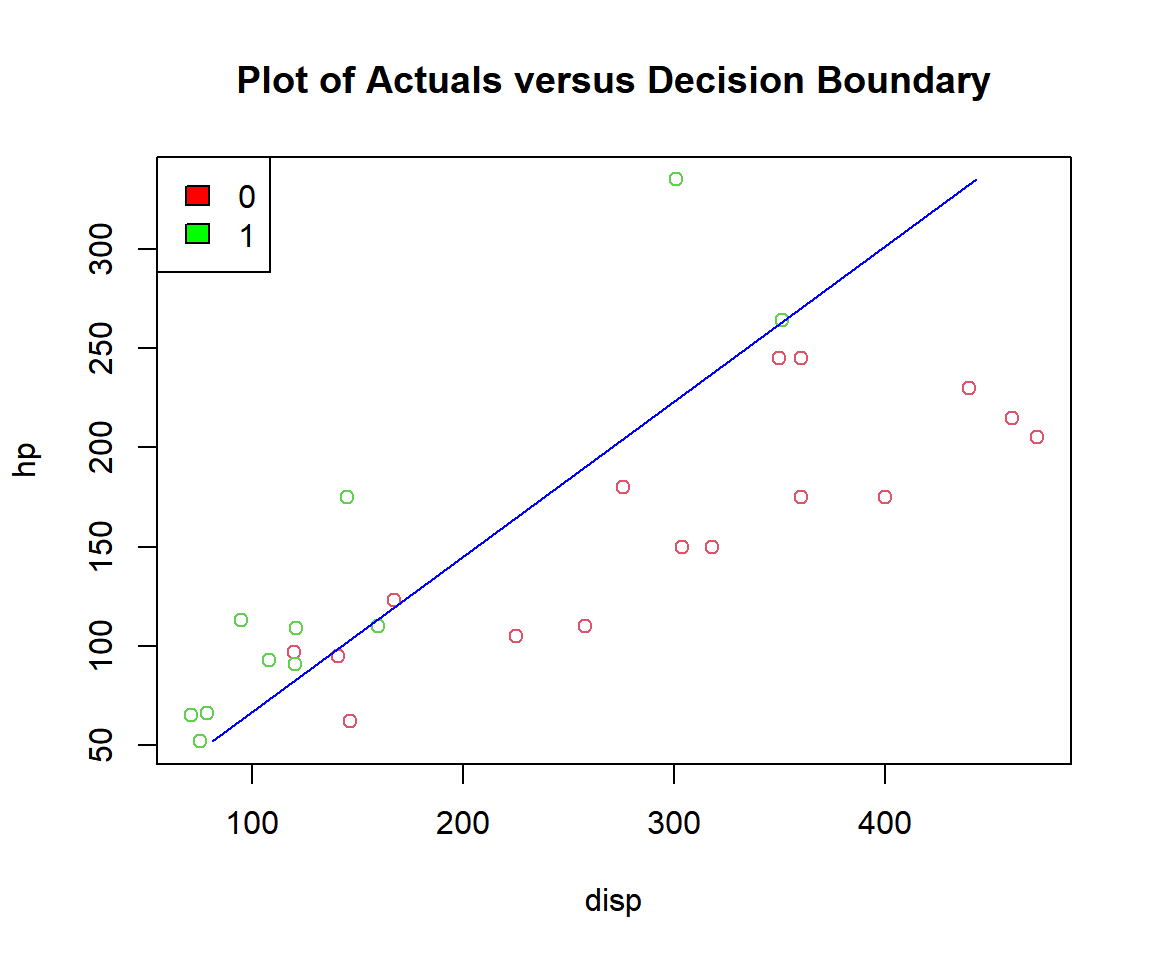
Plot of Logistic Regression Decision Boundary in R

Plot of Logistic Regression Decision Boundary in R

Above, the greens are "1", and the reds are "0".

Interpretation of the Results

  • Coefficients:
    • The estimated coefficient for "disp" is \(\text{summary(model)\$coefficients[2, 1]}\) \(= -0.09518\).
    • The estimated coefficient for "hp" is \(\text{summary(model)\$coefficients[3, 1]}\) \(= 0.1217\).
  • P-values:
    For level of significance, \(\alpha = 0.05\).
    • The p-value for "disp" is \(\text{summary(model)\$coefficients[2, 4]}\) \(= 0.04739\). Since the p-value is less than \(0.05\), we say that "disp" is a statistically significant predictor of the dependent variable \(y\) ("am") or probability of success (automatic transmission = "1").
    • The p-value for "hp" is \(\text{summary(model)\$coefficients[3, 4]}\) \(= 0.07254\). Since the p-value is greater than \(0.05\), we say that "hp" is NOT a statistically significant predictor of the dependent variable \(y\) ("am").
  • AIC:
    The AIC value is \(\text{summary(model)\$aic}\) \(= 22.713\).
    When comparing the model to other models for predicting "am" based on the same data, the model with a lower AIC is better.

Odds

With \(p_{am} = \text{Probability(am = 1)}\).

\(\log \left(\frac{\widehat p_{am}}{1- \widehat p_{am}} \right)\) \(= \widehat \beta_{intercept} + \widehat \beta_{disp} \times disp + \widehat \beta_{hp} \times hp.\)

Hence, the odds, \(\frac{\widehat p_{am}}{1 - \widehat p_{am}}\), is \(\exp \left( 1.40342 + -0.09518 \times disp + 0.1217 \times hp \right).\)

Therefore, for 1 unit increase in \(x_1\) ("disp"), the odds is multiplied by \(\exp (-0.09518)\) \(= 0.909\).

Also, for 1 unit increase in \(x_2\) ("hp"), the odds is multiplied by \(\exp (0.1217)\) \(= 1.129\).

Prediction and Estimation

The estimated \(p_{am} = \text{Probability(am = 1)}\) is, \(\widehat p_{am}\) \(= \frac{\exp (1.40342 \; + \; (-0.09518) \times disp \; + \; 0.1217 \times hp)}{1 \; + \; \exp (1.40342 \; + \; (-0.09518) \times disp \; + \; 0.1217 \times hp)}\).

For example, for \(x_1 = 240\) (240 cu. in. of displacement), and \(x_2 = 160\) (160 horsepower):
\(\widehat p_{am}\) \(= \frac{\exp (1.40342 \; + \; (-0.09518) \times 240 \; + \; 0.1217 \times 160)}{1 \; + \; \exp (1.40342 \; + \; (-0.09518) \times 240 \; + \; 0.1217 \times 160)}\) \(= \frac{\exp (-1.967)}{1 \; + \; \exp (-1.967)}\) \(= 0.123\).

With \(\widehat p_{am} = 0.123\), which is less than \(0.5\), we should predict \(am = 0\), that is, transmission is automatic.

Copyright © 2020 - 2024. All Rights Reserved by Stats Codes